Structural Equation Modeling

Structural equation modeling (SEM) is a modeling framework that makes use of multiple prediction equations. It is also also known as covariance structure analysis, analysis of moment structures, or analysis of linear structural relationships.

Description

SEM is used for measurement error adjustment.

The first component is the measurement model, which is essentially a CFA. Terminology is also common between the two, e.g. factors, factor loadings, indicators, and so on. The most important distinction is that a causal direction is assumed; note the arrows below:

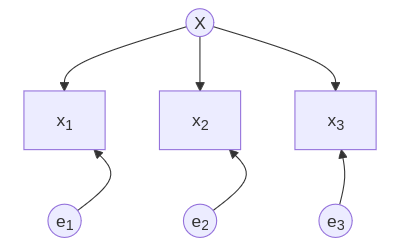
This is equivalent to a formulation like:

• X = α₁ + β₁x₁ + e₁

• X = α₂ + β₂x₂ + e₂

• X = α₃ + β₃x₃ + e₃

The second component is the structural model which specifies the mediation relationship of the latent factors. The simplest formulation would be Y = α_Y + β_YX + e_Y, but...

• there can be multiple predictive factors, e.g. Y ~ X + Z

• the outcome can itself have a measurement model, e.g. Y ~= y1 + y2 + y3

Most model estimation strategies require assuming:

1. a uniform variance for the outcome construct's error, i.e. e,,Y,,.

2. a uniform variance for the latent constructs, e.g. X

CategoryRicottone