|
Size: 484
Comment: Width
|
Size: 1086
Comment: Clarifications and content
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 13: | Line 13: |
| Binary outcomes necessitate a linear model that is bounded between 0 and 1. The '''logistic function''' forms the structure of this model. | Outcomes are coded as 0 and 1. A linear model is constructed (as '''''x''' = '''Xb''''') to predict outcomes using one or more independent variables. |
| Line 15: | Line 15: |
| {{attachment:function.svg}} | The intention of the model is to predict the probability of outcome 1. As always, a probability must be a number between 0 and 1. The linear model as specified can produce any number, however. To connect the linear model to expected values, the '''logistic function''' is used as a [[Econometrics/GeneralizedLinearModel#Design|link function]]. {{attachment:function1.svg}} |
| Line 21: | Line 23: |
| The fitted parameters of this model are in terms of '''logits''' or '''log odds'''. The '''logit function''' is the inverse of the logistic function. {{attachment:function2.svg}} To be clear: ''logistic(x) = p'' and ''logit(p) = x''. |
Logistic Model
A logistic model is a linear regression method for a binary outcome.
Contents
Design
Outcomes are coded as 0 and 1. A linear model is constructed (as x = Xb) to predict outcomes using one or more independent variables.
The intention of the model is to predict the probability of outcome 1. As always, a probability must be a number between 0 and 1. The linear model as specified can produce any number, however. To connect the linear model to expected values, the logistic function is used as a link function.
This function plots as an S-shaped line, so is sometimes called a sigmoid function.
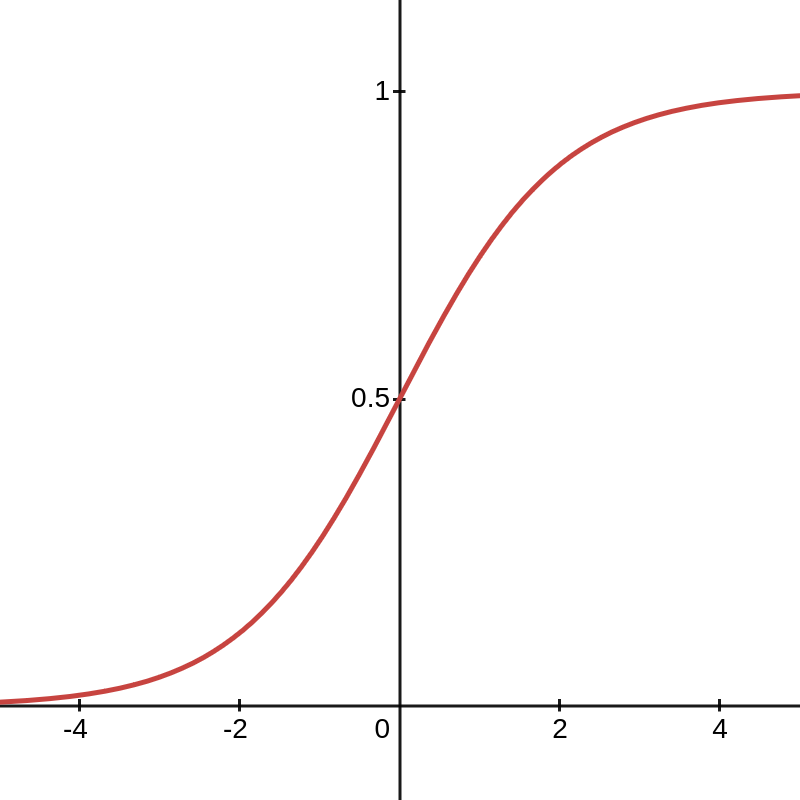
The fitted parameters of this model are in terms of logits or log odds. The logit function is the inverse of the logistic function.
To be clear: logistic(x) = p and logit(p) = x.
