|
Size: 473
Comment: Initial commit
|
Size: 1438
Comment: Killing Econometrics page
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| ## page was renamed from Econometrics/LogisticModel | |
| Line 13: | Line 14: |
| Binary outcomes necessitate a linear model that is bounded between 0 and 1. The '''logistic function''' forms the structure of this model. | A logistic model is selected over any other model when the outcomes are binary. Such outcomes can be coded as 0 and 1 and are assumed to follow a [[Statistics/BinomialDistribution|binomial distribution]]. |
| Line 15: | Line 16: |
| {{attachment:function.svg}} | A linear model is constructed (as '''''y''' = '''Xb''''') to predict outcomes using one or more independent variables. As suggested by the binomial distribution, the intention of the model is to predict the probability of outcome 1 (''p''). And as always, a probability must be a number between 0 and 1. The linear model as specified can produce any number, however. To connect the linear model to the expected values, the '''logistic function''' is used as a [[Econometrics/GeneralizedLinearModel#Design|link function]]. {{attachment:function1.svg}} |
| Line 19: | Line 24: |
| {{attachment:plot.png}} | {{attachment:plot.png||width=300}} The ''x'' term here expands to the entire linear model. The fitted parameters of the model then are in terms of '''logits''' or '''log odds'''. The '''logit function''' is the inverse of the logistic function. {{attachment:function2.svg}} To be clear: ''logistic(x) = p'' and ''logit(p) = x''. |
Logistic Model
A logistic model is a linear regression method for a binary outcome.
Contents
Design
A logistic model is selected over any other model when the outcomes are binary. Such outcomes can be coded as 0 and 1 and are assumed to follow a binomial distribution.
A linear model is constructed (as y = Xb) to predict outcomes using one or more independent variables.
As suggested by the binomial distribution, the intention of the model is to predict the probability of outcome 1 (p). And as always, a probability must be a number between 0 and 1. The linear model as specified can produce any number, however. To connect the linear model to the expected values, the logistic function is used as a link function.
This function plots as an S-shaped line, so is sometimes called a sigmoid function.
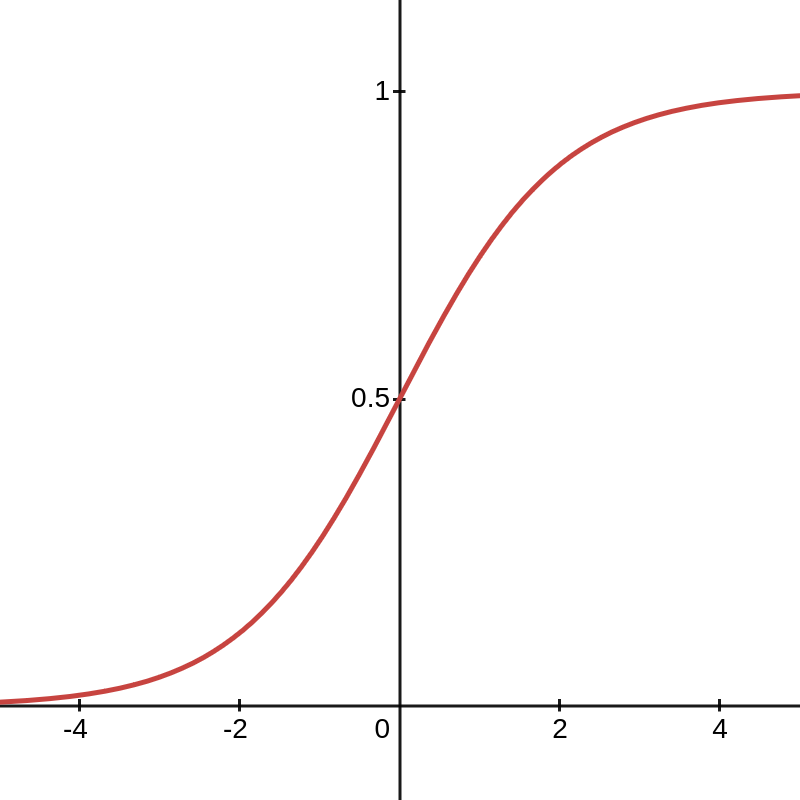
The x term here expands to the entire linear model.
The fitted parameters of the model then are in terms of logits or log odds. The logit function is the inverse of the logistic function.
To be clear: logistic(x) = p and logit(p) = x.
